連載
一覧Pythonで親しむデータ分析と確率モデル【第5回】―確率モデルと検定-前編―

岡本 安晴(おやもと やすはる) 日本女子大学名誉教授
科学は真理を探究するものである。物理学者の本、例えばロベェッリ(栗原訳)「すごい物理学講義」を読めば、真理探究の情熱が伝わってくる。しかし、統計学の本には、ほとんどのデータ分析における確率モデルは完全な正しいものであるとは言えない(Gelmanら、2014、p.142)とか、全てのモデルは間違っている(Martin、2018、p. 181)と書かれている。統計分析におけるモデルは、データから情報を取り出すために設定されるものと考えられる。確率モデルに基づく統計的検定と呼ばれている方法について説明する。なお、本文中のスクリプトはプログラムの一部であることが多いが、プログラムの完全なスクリプトは筆者のウェブサイトhttp://y-okamoto-psy1949.la.coocan.jp/samplefiles/gentosha/に上げておいた。
2つの国からそれぞれ10人の男性をランダムに選び身長のデータを採ったところ、表1のデータを得たとする。

平均値と標準偏差(SD)を求めるため、以下のスクリプトを用意した。
A = np.array([168, 171, 168, 167, 164, 172, 154, 174, 166, 166])
B = np.array([185, 181, 180, 187, 176, 182, 171, 176, 176, 184])
meanA = A.mean()
meanB = B.mean()
sdA = A.std()
sdB = B.std()
print(‘A国: 平均 = ‘, meanA, ‘ SD = ‘, sdA)
print(‘B国: 平均 = ‘, meanB, ‘ SD = ‘, sdB)
実行すると次の出力を得る。
A国: 平均 = 167.0 SD = 5.215361924162119
B国: 平均 = 179.8 SD = 4.728636167014756
A国の平均は167.0㎝、B国の平均は179.8㎝である。この平均値からA国とB国とで身長の平均値に差があるといえるかという問題について考える。
上の2国の平均の差が、サンプリングによるランダムな変動の結果に過ぎないのかどうかを検討するため、同じ平均と標準偏差の集団からランダムに10人分を選んだとき、10人のデータはデータを採るごとにどれくらい変動するか調べる。
平均170、標準偏差6の正規分布から10人分のデータを採ることは次のスクリプトで表される。確率分布として正規分布を設定するのは、標準的な方法である。
mu = 170
sgm = 6
data = scipy.stats.norm.rvs(loc = mu, scale = sgm, size = 10)
print(data)
このスクリプトを実行すると以下のような出力を得る。
[155.35539555 166.85505938 168.27968975 164.37584924 173.6060887
168.17626898 167.59994669 169.47025926 175.36658592 172.76634689]
この10人のデータを採るというサンプリングを5回行うスクリプトを次のように用意した。
data = []
for i in range(5):
data.append(scipy.stats.norm.rvs(loc = mu, scale = sgm, size = 10))
得られた5回のサンプリングを紐図で表示するため、以下のスクリプトを用意した。
Values = []
Groups = []
for i in range(5):
Values += [v for v in data[i]]
Groups += [‘S-{}’.format(i + 1)] * len(data[i])
seaborn.stripplot(x = ‘G’, y = ‘V’, data = {‘G’: Groups, ‘V’: Values})
plt.show()
実行すると図1のグラフが表示される。各回ごとにデータの分布に変動があることがわかる。
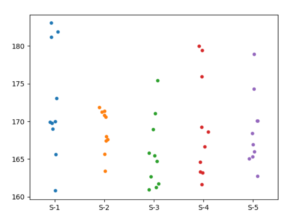
図1 5回のサンプリングの紐図
同じサンプリングのデータに対して、箱図を描くと図2のようになる。
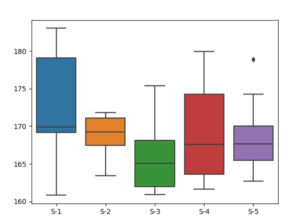
図2 図1の紐図を箱図で表したもの
スクリプトは以下のように用意した。
seaborn.boxplot(x = ‘G’, y = ‘V’, data = {‘G’: Groups, ‘V’: Values})
図1あるいは図2から、同じ集団から採ったデータであっても、サンプリングごとに分布がかなり変動することがわかる。では、平均が同じ集団から採られたデータの平均値の差はどの程度変動するのかが問題になる。表1のデータにおけるA国とB国の平均値の差が、集団の平均値が同じものから得られたと考えられるのか、あるいは異なる平均値からのものと考える方が適切なのか。これを検討するために、シミュレーションを行う。平均値の差は、標準偏差が大きいと変動しやすいので、この影響を除くため、平均値の差をその標準偏差で割ったものについて調べる。これをtとおくと

であるが、具体的な式は以下に示すものである(岡本、2009、pp. 66-68)。
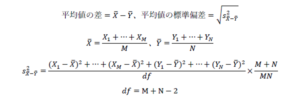
ここで、dfは自由度と呼ばれているものである。
表1のデータに対して上のt値を次のスクリプトで求める。
def calc_t(X, Y):
M = len(X)
N = len(Y)
df = M + N – 2
meanX = X.mean()
meanY = Y.mean()
ss = (((X – meanX) ** 2).sum() + ((Y – meanY) ** 2).sum()) / df
ss_XY = ss * (M + N) / (M * N)
t = (meanX – meanY) / (ss_XY ** 0.5)
return t, df
t, df = calc_t(A, B)
print(‘t = ‘,t, ‘ 自由度 = ‘, df)
実行すると次の出力を得る。
t = -5.454633501380512 自由度 = 18
このt値≈-5.45から、平均値に差があることをどの程度の確信をもっていえるのかを検討するためのシミュレーションを行う。平均170、標準偏差6の集団から10人ずつのデータを2グループ取り、上のt値を求めるということを10000回行う。このためのスクリプトを以下のように用意した。
def calc_t(X, Y):
M = len(X)
N = len(Y)
df = M + N – 2
meanX = X.mean()
meanY = Y.mean()
ss = (((X – meanX) ** 2).sum() + ((Y – meanY) ** 2).sum()) / df
ss_XY = ss * (M + N) / (M * N)
t = (meanX – meanY) / (ss_XY ** 0.5)
return t, df
mu = 170
sgm = 6
M = 10
N_Exp = 10000
t_values = []
for t in range(N_Exp):
X = scipy.stats.norm.rvs(loc = mu, scale = sgm, size = M)
Y = scipy.stats.norm.rvs(loc = mu, scale = sgm, size = M)
t, df = calc_t(X, Y)
t_values.append(t)
上の10000回のt値のサンプリングのヒストグラムを次のスクリプトで描いた。
t_range = [v for v in np.arange(-4, 4, 0.25)]
p_values = [scipy.stats.t.pdf(t, 2 * M – 2) for t in t_range]
plt.hist(t_values, bins = t_range, density = True)
plt.plot(t_range, p_values, linewidth = 3)
plt.plot([-5.45, -5.45], [0.0, 0.1], ‘r-o’, linewidth = 5, label = ‘t = -5.45’)
plt.legend()
plt.show()
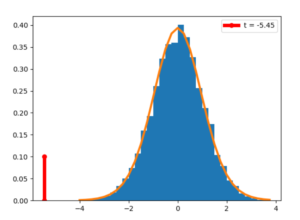
図3 tのヒストグラム
このスクリプトを実行すると図3のグラフが表示される。赤の曲線は、自由度10+10-2=18のt分布の確率密度関数のグラフである。すなわち、差がないという仮定の下では、t値はt分布に従う。図中、赤の縦線はt=-5.45の位置を示すが、この値は表1の2国の差についての値である。「平均値に差がない」というモデル(帰無仮説と呼ばれている)の下で導かれるtの値の分布から左にかなり離れている。帰無仮説が正しいとすると、生起確率の非常に低い値が得られたことになるので、「平均値に差がある」(対立仮説と呼ばれている)と考えた方がよい、すなわち帰無仮説は棄却した方がよいとなる。
次回は、「平均値に差がある」という仮定におけるt値の分布について説明する。
引用文献
-Conover, W. J. (1999). Practical nonparametric statistics, 3rd edition. John Wiley & Sons, Inc.
-Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2014). Bayesian data analysis, 3rd edition. CRC Press.
-Martin, O. (2018). Bayesian analysis with Python, 2nd edition. Packt Publishing.
-岡本安晴(2009).データ分析のための統計学入門。おうふう.
-ロベェッリ(栗原俊英訳、竹内薫監訳)(2017).すごい物理学講義.河出書房新社.(原書:Carlo Rovelli (2014). La realtà non è come ci appare. Scienza E Idee)
