連載
一覧Pythonで親しむデータ分析と確率モデル【第4回】―データの分布と確率モデル―

岡本 安晴(おやもと やすはる) 日本女子大学名誉教授
データに不確実性が伴うとき、そのモデル化に確率分布が用いられることがある。確率モデルとして、ベルヌーイ分布、二項分布、正規分布、カイ二乗分布、t分布、F分布、幾何分布、指数分布、ポアッソン分布、カテゴリカル分布、多項分布等、様々なものが挙げられる。前回に続き、各モデルの概要を説明する。なお、本文中のスクリプトはプログラムの一部であることが多いが、プログラムの完全なスクリプトは筆者のウェブサイトに上げておいた。
幾何分布
時刻を整数値で表す。時刻0、時刻1、時刻2、……というように表すが、過去に遡るときは負の整数値を用いる。あるウェブサイトへのアクセスが各時刻tにおいて確率pで生起するとする。事象が各時点で独立に確率p=0.1で生起するときの生起の様子は、次のスクリプトでシミュレーションできる。
p = 0.1
for t in range(100):
if np.random.uniform() < p: >
print(‘1’, end = ”)
else:
print(‘0’, end = ”)
ここで、np.random.uniform()は、0から1までの範囲に一様に分布する数値を返す乱数発生の関数である。このスクリプトを実行すると以下の出力を得る。
0000000100010100000000001000000000000000000000000100000000000000000000000000000000100000000000000000
事象の生起が1で、生起しなかったことが0で表されている。事象の生起間隔は1から次の1までの間である。間隔が狭いところと広いところがある。次の事象の生起が時刻t後である確率は次式で表される。ただし、直後の時刻から数え、直後の時刻を時刻0とする。
![]()
上の確率は、幾何分布と呼ばれている。
この時間間隔を与える乱数は、次の関数で生成できる。
def w_time():
t = 0
while True:
if np.random.uniform() < p: >
break
t += 1
return t
この乱数を生成してヒストグラムを描くスクリプトを次のように用意した。
n_samples = 10000
p = 0.1
data = []
for i in range(n_samples):
data.append(w_time())
plt.hist(data, density = True, bins = 20)
スクリプトを実行すると、図1のグラフが得られる。幾何数列(等比数列)的に減少していることが分かる。赤の曲線は、このヒストグラムを近似する指数分布の確率密度関数である。指数分布は次節で説明する。
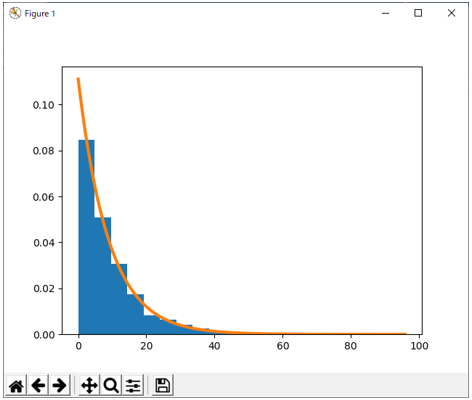
図1 幾何分布と指数分布
指数分布
幾何分布における時刻を連続な時間に替えたとき、幾何数列の替わりに指数関数を用いることになり、指数分布が得られる。指数分布は次式で与えられる。
![]()
指数分布の平均値は
平均=1/β
であり、幾何分布の平均値は
![]()
である。
2つの平均値が等しい
![]()
と置くと、
![]()
を得る。
図1の赤の曲線は、以下のスクリプトによって描かれている。
def exp_d(t, b):
return b * np.exp(-t * b)
b = p / (1.0 – p)
max_data = max(data)
t_range = [t for t in np.arange(0, max_data, 0.1)]
probs = [exp_d(t, b) for t in t_range]
plt.plot(t_range, probs, linewidth = 3)
指数分布には、時間軸上、生起確率が一定であるという性質がある。時刻tまでに事象の生起がなかったという条件のもとで時刻sにおける確率密度関数を求めると
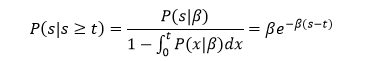
となる。すなわち、時刻tを起点とした元の指数分布と同じパラメータβをもつ指数分布である。
事象の生起間の時間の分布が与えられると、ある時間内に事象の生起する度数の分布を得ることができる。例えば、ある時間内におけるウェブサイトへのアクセス数を確率的に記述することができる。いま、事象の生起間隔が平均1⁄10、すなわちβ=10の指数分布に従うときに、時間1の間(1以外でもよいが、ここでは時間の長さを1としておく)に事象が生起する回数を返す関数を次のように用意する。
def my_poisson(b):
c = 0
v = np.random.exponential(1/b)
while True:
if v > 1:
break
v += np.random.exponential(1/b)
c += 1
return c
ここで、numpy.random.exponential(b0)は、β=1/b0の指数分布に従う乱数を生成する関数である。
いま、乱数生成関数my_poissonによる乱数を生成して、それらのヒストグラムを描くスクリプトを次のように用意した。
b = 10
data = []
for i in range(10000):
data.append(my_poisson(b))
data = np.array(data)
max_v = data.max()
x_rng = np.arange(-0.5, max_v + 1, 1.0)
plt.hist(data, density = True, bins = x_rng)
このスクリプトを実行すると図2のヒストグラムを得る。図中の赤い折れ線はポアッソン分布の確率分布を表している。ポアッソン分布は、次節で説明する。
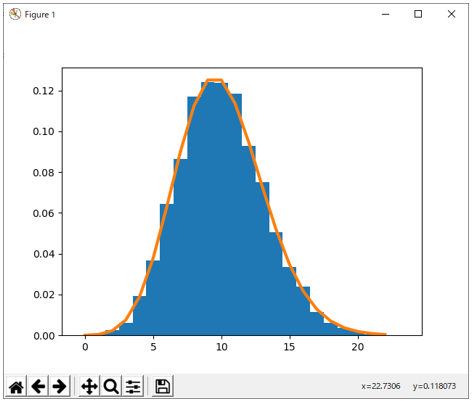
図2 時間1内の事象の生起回数のヒストグラムとポアッソン分布
ポアッソン分布
ポアッソン分布の確率分布は次式で与えられる。
![]()
ポアッソン分布の平均値は
平均値=λ
である。
ポアッソン分布の確率(離散質量関数)は、scipy.statsのオブジェクトpoissonのメソッドpmfで得ることができる。次のコード
scipy.stats.poisson.pmf(v, b)
で、パラメータλ=bのポアッソン分布のvの確率が返される。
図2の赤い折れ線は、次のスクリプトによって描かれている。
x_range = np.arange(0, max_v)
ck_pssn = [scipy.stats.poisson.pmf(v, b) for v in x_range]
plt.plot(x_range, ck_pssn, linewidth = 3)
ポアッソン分布は、度数データの分析に用いられることがある。
最後に、カテゴリカル分布と多項分布について説明する。
カテゴリカル分布
ベルヌーイ分布では、事象は2つ、例えばコインの表と裏、であったが、サイコロの目の数のように3つ以上の場合はカテゴリカル分布と呼ばれる。事象の数がK個であるとき、各事象を1からKまで整数値で表しても一般性は失われない。この場合、確率変数Xは1からKまでの整数値をとる。カテゴリカル分布の確率を
![]()
とおけば、
![]()
である。
カテゴリカル分布の乱数は、numpy.random.choiceによって得ることができる。次のコードにより、カテゴリのリストで指定した項目から確率のリストで指定した確率に従ってサンプル数で指定した数の項目がランダムに返される。パラメータsizeを省略すると1個が返される。
numpy.random.choice(カテゴリのリスト, p = 確率のリスト, size = サンプル数)
例えば、次のスクリプトを用意する。
v = np.random.choice([1,2,3,4,5,6], p = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], size = 10)
print(v)
v = np.random.choice([‘A’, ‘B’], p = [2/3, 1/3], size = 10)
print(v)
実行すると、以下の出力を得る。
[6 4 4 3 2 3 2 5 3 1]
[‘A’ ‘B’ ‘A’ ‘B’ ‘A’ ‘B’ ‘A’ ‘A’ ‘B’ ‘A’]
次のスクリプトは、カテゴリ分布に従う乱数を10000個呼び出してグラフを描くものである。
data = np.random.choice([1,2,3,4,5,6], p = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], size = 10000)
xindx = [1,2,3,4,5,6]
plt.hist(data, bins = [0.5 + v for v in range(7)])
実行すると図3に示すようなグラフが描画される。
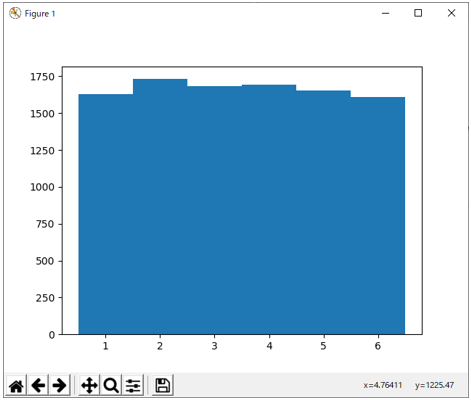
図3 カテゴリカル分布からのサンプリング
多項分布
カテゴリカル分布に従う試行をN回繰り返したときの各カテゴリの度数の分布である。カテゴリがK個あり、N回の試行中、カテゴリkの度数が![]() 個である確率は、カテゴリkの確率を
個である確率は、カテゴリkの確率を![]() とおくと、次式で与えられる。
とおくと、次式で与えられる。
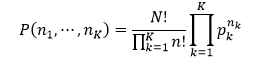
多項分布の乱数はnumpy.random.multinomialを次の形で呼び出せば生成できる。
numpy.random.multinomial(N, [p1, …, pK], size = サンプル数)
確率のリスト[p1, …, pK]は![]() を表している。パラメータsizeを省くと1とみなされる。
を表している。パラメータsizeを省くと1とみなされる。
次のスクリプトを用意してみる。
v = np.random.multinomial(3, [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], size = 10)
print(v)
実行すると以下の出力を得る。
[[0 1 0 0 0 2]
[0 2 0 1 0 0]
[1 0 0 0 2 0]
[0 1 1 1 0 0]
[0 1 0 0 0 2]
[0 0 0 0 2 1]
[2 1 0 0 0 0]
[0 2 0 0 1 0]
[2 0 0 0 0 1]
[0 1 2 0 0 0]]
サンプルを多数とって分布を確認するために、以下のスクリプトを用意した。
data = np.random.multinomial(3, [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], size = 10000)
freqs = data.sum(axis = 0)
plt.bar(range(1,7), freqs)
実行すると図4のようなグラフが表示される。
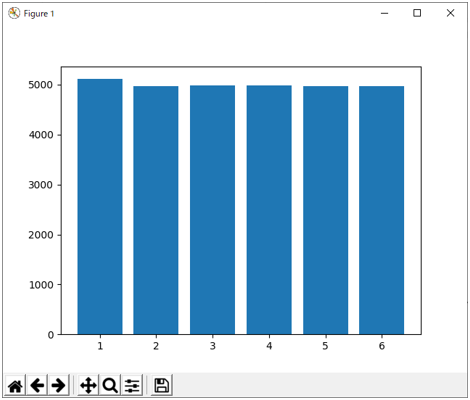
図4 多項分布のサンプリング例
次回は、データに含まれる不確実性を確率モデルで表した統計学的検定について説明する。
